Lommeregner til at beregne antal besvarelser

Herunder kan du se, hvor mange besvarelser du skal indsamle for at få valide data i din spørgeskemaundersøgelse.

Du skal indtaste din population. Det er antallet af mennesker, som er i din målgruppe. Undersøger du fx. en tendens blandt danmarks 15.000 revisorer, så skal du indtaste 15.000. Er det blandt Viborgs 41.621 indbyggere, så er det tallet du skriver ind.

Definitionen På En Stikprøve

Indenfor statistik er en stikprøve et uddrag af en samlet målgruppe. Stikprøven bruges i forbindelse med markedsresearch og definerer antallet af individer, som bør inkluderes i en given stikprøve. Har man en tilpas stor stikprøve, kan man argumentere for at ens data er statistisk valid; men, en for stor stikprøve koster tid og penge. Så, hvordan finder du ud af, hvor stor stikprøven skal være?

Hvordan Bestemmer Man En Stikprøvestørrelse

Når du tager en stikprøve har du brug for at dyppe fødderne i lidt statistik. Det er for at forstå de valg, som du skal træffe. En enkel formel vil hjælpe dig med at holde hovedpinepillerne på afstand og give dig et tal, som er let at forholde sig til.

Der er nogle få ting, som du skal kende til, for at du kan beregne stikprøvens nødvendige størrelse:

1. Målgruppens størrelsen

Målgruppen bliver også kaldt for Populationen. Det er antallet af mennesker, som passer på dine demografiske kriterier. Hvis du vil dykke ned i et emne, som berører alle mødre i Danmark, så vil din population være antallet af mødre i Danmark. Din population behøver ikke være i den størrelsesorden. Du skal dog vide, hvor mange mennesker, som stemmer overens med din demografi.

Det er helt okay, hvis du ikke kender det præcise antal. Det er meget normalt, at man ikke kender populationen og i det tilfælde må man lave et kvalificeret gæt.

2. Konfidensinterval – hvor sikker vil du være?

Der er ingen stikprøve, som er perfekt. Du skal derfor bestemme dig for, hvor mange fejl du tillader. Konfidensintervallet afgører, hvor meget større eller mindre din stikprøves gennemsnit må være ift. din population.

Hvis du har set megafonmålinger op til valget, så vil der altid stå, at ”71 % af vælgerne vil stemme på Peter Petersen, med en usikkerhed på +/- 5 %.”

Det mest normale konfidensinterval er 95 %, hvilket betyder, at du er 95 % sikker på, at dine data er korrekte.

3. Standardafvigelse – hvor meget varians forventer du i dine besvarelser?

Eftersom vi ikke ved, hvor varierede vores besvarelser vil være, så kan vi ikke svare på det endnu. Du kan dog med ro i maven vælge 50 % afvigelse i dine resultater – det er et meget konservativt nummer, som tager højde for stor afvigelse i dine data. Så, selvom der skulle være stor afvigelse i dine data, så vil du stadig have en tilpas stor stikprøve til at dine data vil være valide.

Vi bruger ofte tallet 0,5 som standard.

Hvordan Beregner Man En Stikprøves Størrelse?

Super. Nu har vi det basale på plads – og nu er det tid til at beregne de reelle tal.

Dit konfidensinterval afspejler en såkaldt Z-score. Det er en konstant værdi, som du skal bruge i din beregning. Her er Z-scoren for de mest almindelige konfidensintervaller.

Det næste vi skal gøre, er at sætte vores tal ind i formlen for beregning af stikprøvestørrelse.

Formlen ser sådan ud:

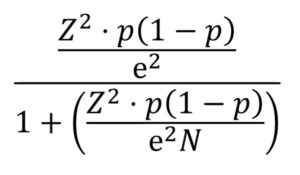
Ligningen ser voldsom ud, men læg mærke til, at det stort set er det samme, som er over divisionstegnet som under. Det eneste, som er ekstra under divisionstegnet er 1 og N.

Ligesom med talemåden ”hvordan spiser man bedst en elefant? I små bidder” så handler det om at tage det med ro.

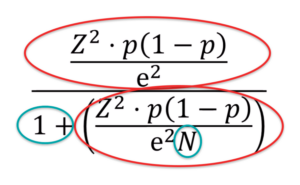
Det ser voldsomt ud, men meget af det går igen.

Du kan enten skrive det hele ind på én gang

Eller dele den op i to regnestykker:

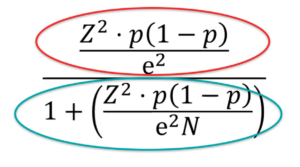
Rød Cirkel

Blå Cirkel

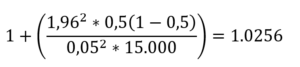
Som kan divideres med hinanden

Og nu har du beregnet, at hvis du vil drage konklusioner på tværs af 15.000 revisorer, som med 95 % sandsynlighed er korrekte, så skal du have 375 svar.

Skal du hurtigt bruge et tal, så kan du bare bruge vores lommeregner i toppen, hvor du bare skal indtaste størrelsen på din population ind, hvorefter du vil få at vide, hvor mange svar du skal bruge, for at kunne drage konklusioner med 95 % sandsynlighed.

Virker det som mange svar at indsamle?

Du kan altid indsamle færre svar, men det betyder bare at fejlmargen bliver større og risikoen for at de data du indsamler ikke er gældende for hele populationen, stiger.

Med Smartevaluering kan du let dele din evaluering via Besvar.nu med en 4 cifret kode, via SMS eller et unikt link – så nu er det enkelt at få besvarelserne i hus.